Agrietado! (platón huevo) rompecabezas en 3D para imprimir
2160 Visualizaciones 4 Me gusta 0 Descargas realizadas Descarga aqui la pieza desde 3dforprint
http://www.johnrausch.com/DesignCompetition/2015/default.htm#08
Le...er más sobre la historia detrás de este puzzle en el 'Cómo he Diseñado Esta sección
El rompecabezas se compone de tres capas anidadas de dodecaedros.
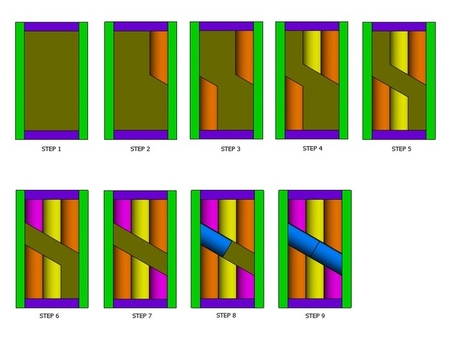
El reto es romper Platón huevo en sus partes constituyentes, encontrar y desmontar el trisected dodecaedro en el centro, a continuación, poner de nuevo juntos de nuevo.
Cada una de las tres etapas que requiere un grado de coordinar el movimiento.
El blanco del huevo es particularmente difícil de desmontar con la mano, pero fácilmente se separan haciendo girar el huevo sobre la mesa.
Usted deberá imprimir:
3 de la Shell de piezas en marrón claro
2 de la Blanco de piezas en blanco o claro
2 de la Blanca B piezas en blanco o claro
3 de la Yema de piezas en amarillo
Si te gusta este rompecabezas, por favor considere dejar un tip que me animan a compartir más de mi rompecabezas.
Impresora:
Mendel90
Balsas:
No
Apoya:
No
Resolución:
0.15 a 0.2 mm
Relleno:
25%
Notas:
Este es un truc...o de impresión que necesita un bien afinado de la impresora. Si su impresora es la extrusión, las piezas NO encajan. Ningún material de apoyo debe ser requerida por cualquiera de las piezas, pero que sin duda tendrá una buena parte de ventilador de refrigeración.
Cómo He Diseñado Este
La idea de este rompecabezas venía de hacer una pregunta simple: ¿la superficie de un dodecaedro todos se subdivide en un número de idénticas partes entrelazadas? Debido a que el dodecaedro tiene 12 caras, hay cuatro posibles maneras de dividir estos en grupos iguales. Pronto descubrí que las dos piezas cada uno con una cadena de seis caras pentagonales sería enclavamiento pero imposible de separar. También decidí que seis piezas cada uno con dos caras pentagonales no sería una enclavamiento de puzzle. Así que, comencé a experimentar con tres cadenas de cuatro pentágonos y descubrió que era de hecho posible envolver tres formas idénticas sobre la superficie del dodecaedro. Pero las piezas se separan? He utilizado un programa informático para la extrusión de la forma hacia el exterior desde un punto central, convirtiéndola en un objeto sólido. Imprimí tres de estas formas y demostró que podían ser montados en un dodecaedro uso de coordinar un movimiento de deslizamiento. Luego traté de experimentar con cuatro cadenas de tres pentágonos. Era bastante obvio que las cuatro partes podría ser montados en un dodecaedro con bastante facilidad, pero sin enclavamiento, para que no se mantenga unida. Yo tenía la idea de combinar dos conjuntos completos de estas formas, anidados uno dentro del otro. Los tres pentágonos del grupo interno se vio compensado en relación a los tres pentágonos del grupo exterior que permitió que las formas para bloquear juntos. He creado varios diseños que interconectados para formar una completa dodecaedro, pero todos ellos eran imposibles de resolver. En el sexto intento, por fin he conseguido imprimir un conjunto de cuatro piezas que podrían ser montados en un dodecaedro con una coordenada movimiento de deslizamiento. La última etapa creativa fue cuando tuve la idea de combinar los puzzles en un conjunto jerarquizado de las formas de representación de la yema de huevo, blanco y cáscara de un huevo. Puede que la grieta de Platón huevo y poner de nuevo juntos?
Diseñador
richgainDescripción del modelo 3d
Esta es mi entrada para el 2015 IPP de Rompecabezas de la competencia de Diseñohttp://www.johnrausch.com/DesignCompetition/2015/default.htm#08
Le...er más sobre la historia detrás de este puzzle en el 'Cómo he Diseñado Esta sección
El rompecabezas se compone de tres capas anidadas de dodecaedros.
El reto es romper Platón huevo en sus partes constituyentes, encontrar y desmontar el trisected dodecaedro en el centro, a continuación, poner de nuevo juntos de nuevo.
Cada una de las tres etapas que requiere un grado de coordinar el movimiento.
El blanco del huevo es particularmente difícil de desmontar con la mano, pero fácilmente se separan haciendo girar el huevo sobre la mesa.
Usted deberá imprimir:
3 de la Shell de piezas en marrón claro
2 de la Blanco de piezas en blanco o claro
2 de la Blanca B piezas en blanco o claro
3 de la Yema de piezas en amarillo
Si te gusta este rompecabezas, por favor considere dejar un tip que me animan a compartir más de mi rompecabezas.
Parametros de impresión 3d
Configuración De ImpresiónImpresora:
Mendel90
Balsas:
No
Apoya:
No
Resolución:
0.15 a 0.2 mm
Relleno:
25%
Notas:
Este es un truc...o de impresión que necesita un bien afinado de la impresora. Si su impresora es la extrusión, las piezas NO encajan. Ningún material de apoyo debe ser requerida por cualquiera de las piezas, pero que sin duda tendrá una buena parte de ventilador de refrigeración.
Cómo He Diseñado Este
La idea de este rompecabezas venía de hacer una pregunta simple: ¿la superficie de un dodecaedro todos se subdivide en un número de idénticas partes entrelazadas? Debido a que el dodecaedro tiene 12 caras, hay cuatro posibles maneras de dividir estos en grupos iguales. Pronto descubrí que las dos piezas cada uno con una cadena de seis caras pentagonales sería enclavamiento pero imposible de separar. También decidí que seis piezas cada uno con dos caras pentagonales no sería una enclavamiento de puzzle. Así que, comencé a experimentar con tres cadenas de cuatro pentágonos y descubrió que era de hecho posible envolver tres formas idénticas sobre la superficie del dodecaedro. Pero las piezas se separan? He utilizado un programa informático para la extrusión de la forma hacia el exterior desde un punto central, convirtiéndola en un objeto sólido. Imprimí tres de estas formas y demostró que podían ser montados en un dodecaedro uso de coordinar un movimiento de deslizamiento. Luego traté de experimentar con cuatro cadenas de tres pentágonos. Era bastante obvio que las cuatro partes podría ser montados en un dodecaedro con bastante facilidad, pero sin enclavamiento, para que no se mantenga unida. Yo tenía la idea de combinar dos conjuntos completos de estas formas, anidados uno dentro del otro. Los tres pentágonos del grupo interno se vio compensado en relación a los tres pentágonos del grupo exterior que permitió que las formas para bloquear juntos. He creado varios diseños que interconectados para formar una completa dodecaedro, pero todos ellos eran imposibles de resolver. En el sexto intento, por fin he conseguido imprimir un conjunto de cuatro piezas que podrían ser montados en un dodecaedro con una coordenada movimiento de deslizamiento. La última etapa creativa fue cuando tuve la idea de combinar los puzzles en un conjunto jerarquizado de las formas de representación de la yema de huevo, blanco y cáscara de un huevo. Puede que la grieta de Platón huevo y poner de nuevo juntos?